This article discusses how you can solve the Three Reservoir Problem with Excel. First, we develop the governing equations by applying Bernoulli's Equation and the Continuity Equation. We then explore how these equations can be solved in Excel.
If you just want the tutorial spreadsheet, click here, but I encourage you to read the rest of the article so you understand how the spreadsheet was developed. Read on for the Three Reservoir Problem solution.
Theory
Three reservoirs at different elevations are connected by a pipe network. The common junction of the piping network is subject to an external demand Qj of 0.01 m3/s. We will develop the theory required to calculate the flowrates in each pipe (Q1, Q2 and Q3), the head at the junction (Hj) and determine whether liquid is flowing into or out of each reservoirAssuming that the liquid level in each reservoir is constant and the surface is open to atmosphere, the Bernoulli Equation for Reservoir i (where i=1, 2 and 3) is
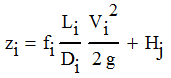 |
| Equation 1 |
But the volumetric flowrate Qi and the cross sectional area Ai of the pipe are
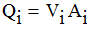 |
| Equation 2 |
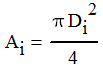 |
| Equation 3 |
Substituting Equations 2 and 3 into Equation 1 to eliminate Vi gives
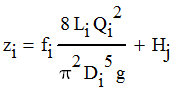 |
| Equation 4 |
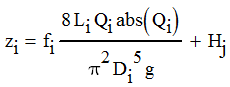 |
| Equation 5 |
We only need a few more relationships to completely specify the system. The friction factor fi is given by the Haaland approximation to the Colebrook-White Equation,
where Rei is the Reynolds Number,
Additionally, the sum of the flowrates from each reservoir is equal to the external demand
Excel Implementation
Moving all terms in Equation 5 to the right-hand side gives
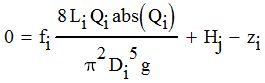 |
| Equation 6 |
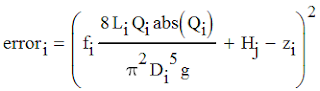 |
| Equation 7 |
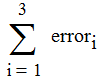 |
| Equation 8 |
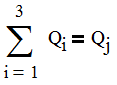 |
| Equation 9 |
Step 2. Set initial guess values for the flowrates in each pipe
Step 3. Specify calculated values
Step 4. Specify an initial guess value for the head at the junction, and the sum of all flowrates in each pipe (as given by Equation 9). The External Demand will act as the constraint for Excel's Solver
Step 5. Specify the errors for each pipeline (as given by Equation 7), and the total error (as given by Equation 8).
We can now use Excel's Solver Add-in to find the flowrates (Q1, Q2 and Q3) and head at the junction (Hj) that minimize the total error (as set in Step 5) subject to the flowrate constraint (as set in Step 4).
Step 6. Initiate Excel's Solver menu (if you haven't already, you'll need to load it in the File > Options > Add-ins menu)
Step 7. Make the appropriate changes in the Solver window such that you minimise the total error by varying the flowrates and the junction head while maintaining the external demand at a set value (for this example, I've set the external demand to 0.01 m3/s). Additionally, set the solving method to GRG Nonlinear.
Step 8. Click Solve. After dismissing the following window, you'll find that the flowrates in each pipeline, and the junction head have changed. Bear in mind that positive flowrates indicate flow out of a reservoir, while negative flowrates indicate liquid flow into a reservoir.
Step 9. We're not finished yet! Check that the Total Error specified in Step 5 is a very small number, and the External Demand (in Step 5) is equal to the value specified in Step 7.











0 comments:
Post a Comment